Московской государственной консерватории им. П.И. Чайковского (Главный научный сотрудник)
Россия
Данная работа посвящена структурным связям музыкальной гармонии пифагорейских квинтовых строев с системой водородных связей в генетических молекулах ДНК. Обнаружены скрытые закономерности в стохастической организации последовательностей водородных связей в геномных ДНК высших и низших организмов. Описанные закономерности являются кандидатами на роль универсальных закономерностей биологической эволюции. Выдвигается положение о фундаментальной роли стохастических закономерностей в генетически наследуемой организации биологических тел. В представленном исследовании использован авторский метод иерархии бинарных стохастик, применяемый в генетических и физиологических исследованиях.
ДНК, пифагорейские музыкальные строи, водородные связи, стохастика, дихотомии, фракталы
ВВЕДЕНИЕ.
Музыка давно связывается с математикой. Например, Лейбниц утверждал, что музыка есть математика души, которая вычисляет сама того не сознавая. При этом Гете полагал, что «музыка – нечто целиком врожденное, нутряное» (https://www.sky-art.com/goethe/ekkerm/ekkerm01.htm). Понятие музыкальной гармонии известно в Европе со времен Пифагора и его пифагорейского строя до-ре-ми-фа-соль-ля-си, основанного на отношении 3/2, которое называется квинтой. Если звуковые частоты этих нот разнести в разные октавы, то образуется фрагмент из 7 членов (ступеней) геометрической прогрессии с квинтой 3/2 как коэффициентом прогрессии. Эти частоты можно свести в одну октаву делением или умножением на 2. При этом внутри одной октавы отношения соседних звуковых частот имеют всего два вида величин (интервалов), то есть этот строй двухинтервальный. Данный двухинтервальный (Инь-Ян) строй был известен в Древнем Китае, где музыка считалась основой мироздания и была развита музыкальная терапия; при этом квинтовые строи предпочитали равномерно-темперированному строю, также известному там.
В общем случае, пифагорейским называется любой строй, который может быть построен на основе отношения квинты 3/2 и октавы 2/1. Примерами таких строев являются пентатоника, тетратоника и тритоника. Известным историческим фактом является то, что эти квинтовые строи использовались разными народами во всем мире задолго до Пифагора без знания каких-либо математических закономерностей в силу врожденной тяги к этим строям. Например, пентатоническая гамма является основой традиционной музыки китайцев, вьетнамцев, монголов, тюркских народов (башкир, татар, чувашей и др.), империи инков и народов Южных Анд в целом. Пентатоника также встречается в европейском музыкальном фольклоре и в древнейших пластах русской народной песни. Тетратоническая музыка была распространена в Полинезии, Меланезии, а также среди множества племен индейцев, проживающих на разных территориях. Тетратонические, а также тритоновые шкалы обычно использовались племенными народами Индии (см. обзор литературы в [1]).
Данный факт врожденного сродства людей с квинтовыми музыкальными строями вызывает вопрос о том, не имеется ли в генетической системе структурных особенностей, которые можно использовать для объяснения этого сродства? При анализе этого вопроса автор обратил внимание на то, что в двойной спирали ДНК комплементарные аденин А и тимин Т сопряжены 2 водородными связями, а комплементарные гуанин G и цитозин С – 3 водородными связями. Поэтому в ДНК любая последовательность нуклеотидов представима как бинарная последовательность цифр 2 и 3 в сложной очередности. Анализ таких последовательностей ранее выявил, что при их рассмотрении как последовательностей фрагментов длины “n” (триплетов, 6-плетов и пр.) возникают семейства произведений водородных связей, величины которых дают отношения частот квинтовых музыкальных строев, подтверждая структурную связь квинтовых строев с генетической информатикой [2]. Продолжение исследований бинарных последовательностей водородных связей в геномных ДНК высших и низших организмов выявило универсальные правила их стохастической организации, некоторые из которых представлены в данной статье.
МАТЕРИАЛЫ И МЕТОДЫ.
Исследованию подвергались геномные ДНК из общедоступного банка генетических данных GenBank (https://www.ncbi.nlm.nih.gov/genbank/). Их анализ проводился авторским методом “иерархии бинарных стохастик”, который заключается в следующем. Бинарная последовательность водородных связей в геномной ДНК (например, последовательность 2332332322…) сначала представляется как последовательность одиночных цифр (2-3-3-2-3-…) и в ней подсчитываются проценты %2 и %3 каждого из двух видов цифр. Затем она представляется как последовательность цифровых дуплетов (23-32-33-23-22…) и подсчитываются проценты %22, %23, %32, %33 всех четырех возможных видов таких дуплетов. Затем эта же бинарная последовательность представляется как последовательность триплетов (233-233-232-…), тетраплетов (2332-3323-…), пентаплетов (23323-32322-)…и т.д. При каждом таком представлении подсчитываются проценты каждого из возможных в нем видов n-плетов [3]. Именно анализ возможных числовых связей между получаемыми семействами процентных величин выявляет универсальные правила дихотомий в стохастической организации геномных ДНК, описываемые ниже.
ПОЛУЧЕННЫЕ РЕЗУЛЬТАТЫ.
В качестве примера результатов такого анализа обратимся к бинарной последовательности водородных связей в ДНК первой хромосомы человека, состоящей примерно из 250 миллионов цифровых звеньев 2 и 3 (эта огромная последовательность сопоставима по объему с текстом 100 романов «Война и мир» Л.Н. Толстого). Анализ полученных феноменологических данных о процентах n-плетов водородных связей (кратко, Н-n-плетов) выявил существование в стохастической организации этой ДНК двух типов связей дихотомического типа между величинами процентов из разных семейств H-n-плетов: семейства на основе алгоритма дихотомий суффиксного типа и семейства на основе алгоритма дихотомий префиксного (приставочного) типа.
Суффиксная дихотомия отражает следующее феноменологическое правило взаимосвязи H-n-плета с такими двумя «дочерними» H-(n+1)-плетами, которые образованы из него добавлением суффиксов 2 и 3: в геномных ДНК сумма процентов таких двух суффикс-дочерних H-(n+1)-плетов практически равна проценту исходного (материнского) H-n-плета.
Например, для последовательностей водородных связей ДНК первой хромосомы человека имеем следующие примерные равенства округленных величин процентов при суффиксной дихотомии (с точностью до четвертого или пятого знака после запятой при представлении процентов как долей единицы):
%2=0,58276 ≈ %22+%23=0,58276; %3=0,41724 ≈ %32+%33= 0,41724;
%22=0,3281 ≈ %222+%223=0,3281; %32=0,25462 ≈ %322+%333=0,25462;
%23=0,2546 ≈ %232+%233 ≈ 0,2547; %33=0,1626 ≈ %332+%333=0,1626;
%222=0,2003 ≈ %2222+%2223=0,2003;
%333=0,06363 ≈ %3332+%3333=0,06364, и так далее.
На основе суффиксной дихотомии имеют место два фрактало-подобных дерева процентов (вероятностей) п-плетов водородных связей в данной хромосомной ДНК (Рис. 1). Из них левое дерево содержит H-n-плеты, начинающиеся с четного числа 2, а правое содержит H-n-плеты, начинающиеся с нечетного числа 3.
|
∑ % |
Проценты H-n-плетов, начинающихся с 2 |
Проценты H-n-плетов, начинающихся с 3 |
∑ % |
|
0,58275 |
%2 |
%3 |
0,4172 |
|
0,58276 |
%23+%22 |
%33+%32 |
0,4172 |
|
0,58278 |
%233+%232+%223+%222 |
%333+%332+%323+%322 |
0,4172 |
|
0,58274 |
%2333+%2332+%2323+%2322 +%2233+%2232+%2223+%2222 |
%3333+%3332+%3323+%3322 +%3233+ %3232+%3223+%3222 |
0,4173 |
|
0,58267 |
%23333+%23332+%23323+ %23322+%23233+%23232+ %23223+%23222+%22333+ %23332+%22323+%22322+ %22233+%22232+%22223 +%22222 |
%33333+%33332+%33323+ %33322+%33233+%33232+ %33223+%33222+%32333+ %32332 +%32323+%32322+ %32233+%32232+%32223 +%32222 |
0,4173 |
Рис. 1. Начала левого и правого фрактальных деревьев дихотомий процентов n-плетов водородных связей ДНК первой хромосомы человека, которые базируются на алгоритме суффиксной дихотомии. Левый и правый столбцы показывают практически инвариантные на всех уровнях каждого дерева значения сумм процентов H-n-плетов в них.
Fig. 1. Beginnings of the left and right fractal dichotomy trees of percentages of n-plets of hydrogen bonds of the first human chromosome DNA, which are based on the suffix dichotomy algorithm. The left and right columns show the values of the sums of the percentages of H-n-plets in them that are practically invariant at all levels of each tree.
Левое и правое дихотомические деревья на Рис. 1 являются комплементарными в том смысле, что при операции комплементарности 2↔3, то есть взаимной замены цифр 2 и 3 в числовых символах всех их Н-n-плетов, эти феноменологические деревья обмениваются составом H-n-плетов. Это напоминает феномен комплементарности нуклеотидов в двойной спирали ДНК (A↔T, C↔G) и реализацию древнего принципа «подобное порождает подобное».
Деревья на Рис. 1 называются фрактальными не только в силу фрактальности их схемной конфигурации, аналогичной схеме дихотомий Инь-Ян древнекитайской «Книги перемен», но также в силу числовой особенности его наборов вероятностей в геномных ДНК: каждый из его членов (то есть процент любого H-n-плета), как это можно проверить, является вершиной его собственного фрактального дерева на основе суффиксной дихотомии процентных величин. Рис. 2 показывает пример такого нового фрактального дерева в случае использования величины %23 в качестве его вершины при алгоритме суффиксной дихотомии H-n-плетов.
|
∑% |
Проценты H-n-плетов, начинающихся с дуплета 23
|
|
0,2546
|
%23
|
|
0,2547 |
%233+%232
|
|
0,2546 |
%2333+2332+%2323+%2322
|
|
0,2546 |
%23333+%23332+%23323+%23322 +%23233+%23232+%23223+%23222 |
Рис. 2. Начало фрактального дерева H-n-плетов, вершиной которого взят %23 и которое построено на основе алгоритма суффиксной дихотомии вероятностей в последовательности водородных связей ДНК первой хромосомы человека. Левый столбец демонстрирует практическую инвариантность суммарной величины процентов на всех уровнях.
Fig. 2. The beginning of the fractal tree of H-n-plets, whose apex is %23 and which is built on the basis of the algorithm of suffix dichotomy of probabilities in the sequence of hydrogen bonds in the DNA of the first human chromosome. The left column demonstrates the practical invariance of the total percentage value at all levels.
Префиксная дихотомия отражает аналогичное феноменологическое правило взаимосвязи H-n-плета с двумя «дочерними» H-(n+1)-плетами, которые образованы из него добавлением приставок 2 и 3 в его начало: в геномных ДНК сумма процентов таких двух префикс-дочерних H-(n+1)-плетов практически равна проценту исходного H-n-плета. Например, для последовательностей водородных связей ДНК первой хромосомы человека имеем следующие примерные равенства округленных величин процентов при префиксной дихотомии:
%2=0,58276 ≈ %22+%32=0,58275; %3=0,41724 ≈ %23+%33=0,41725; %22=0,3281 ≈ %222+%322=0,3281; %32=0,2547 ≈ %232+%332=0,2547; %23=0,2546 ≈ %223+%323=0,2546; %33=0,1626 ≈ %233+%333=0,1626; %222=0,2003 ≈ %2222+%3222=0,2003; %333=0,06363 ≈ %2333+%3333=0,06365, и так далее.
На основе префиксной дихотомии имеют место два других фрактало-подобных дерева вероятностей n-плетов водородных связей в рассматриваемой хромосомной ДНК (Рис. 3), которые отличаются от фрактальных деревьев суффиксной дихотомии на Рис. 1 набором H-n-плетов в них.
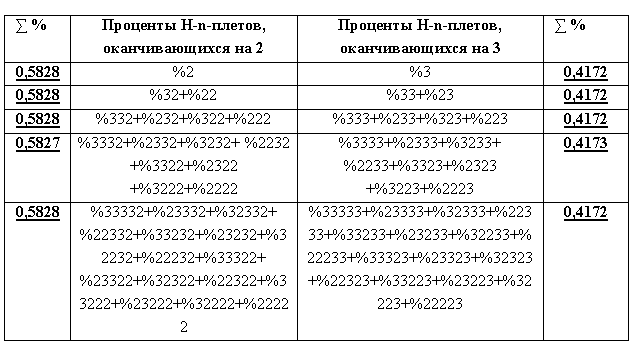
Рис. 3. Начала левого и правого фрактальных деревьев дихотомий процентов H-n-плетов водородных связей ДНК первой хромосомы человека, которые базируются на алгоритме префиксной дихотомии. Левый и правый столбцы показывают практически инвариантные на всех уровнях каждого дерева значения сумм процентов H-n-плетов в них.
Fig. 3. Beginnings of the left and right fractal dichotomy trees of percent H-n-plets of hydrogen bonds in the first human chromosome DNA, which are based on the prefix dichotomy algorithm. The left and right columns show the values of the sums of the percentages of H-n-plets in them that are practically invariant at all levels of each tree.
Геномная информатика оказывается сопряженной с сетями из множества взаимно связанных фрактальных деревьев вероятностей. Выполнение аналогичных правил дихотомий вероятностей в стохастической организации геномных ДНК каждый читатель может проверить, например, на основе опубликованных данных о процентах H-n-плетов первой хромосомы растения Arabidopsis thaliana [3, 4]. Эти и другие правила стохастической организации геномных ДНК установлены и проверены автором на множестве геномных ДНК, включая следующие: всех 24 видов хромосом человека; всех хромосом дрозофилы, мыши, червя, многих растений; 19 геномов бактерий и архей; многих экстремофилов, живущих в экстремальных условиях, например, радиации с уровнем в 1000 раз превышающим смертельный для человека.
Соответственно, эти универсальные правила свидетельствуют о существовании нетривиальных алгебраических инвариантов глобальной геномной природы, которые остаются неизменными на протяжении миллиардов лет биологической эволюции, в ходе которой отмирают миллионы видов организмов и возникают новые (хотя локально геномные секвенции изменяются мутациями, прессом естественного отбора и пр.).
Дихотомии в генетически наследуемых биологических телах и их трансформациях хорошо известны. Их примеры дают, например, функционирование двухнитевой ДНК, митоз соматических клеток, ветвления у растений, бронхиальное дерево легких человека с его 23 уровнями дихотомий, дихотомическое ветвление нейронных аксонов и дендритов. Представленные на Рис. 1 и 3 асимметричные пары из левого и правого фрактальных деревьев, связанные с четным и нечетным числами 2 и 3, ассоциируются с двумя генетически наследуемыми асимметричными полушариями головного мозга, наделенными разными функциями. Сквозная для биологии и культуры тема Инь-Ян (левое и правое, чет и нечет, женское и мужское) систематизирована в изданной на разных языках известной книге с характерным названием «Чет и нечет. Асимметрия мозга и знаковых систем» [5].
Но в геномных ДНК в отличие от телесных конструкций мы встречаемся с принципиально иным типом дихотомии: дихотомиями стохастических (вероятностных) характеристик в информационных последовательностях ДНК. Обширные дихотомические фрактальные сети вероятностей геномных ДНК – это та почва, из которой произрастают живые тела и генетический интеллект. Вещественные структуры живых тел возникают не на пустом месте, а имеют структурные прототипы в закономерной системе биологических вероятностей в многообразии генетических языков с их семействами многопараметрических алфавитов. Здесь надо напомнить, что генетика как наука началась с открытия Менделем правил стохастического (вероятностного) наследования признаков в экспериментах по скрещиванию организмов. Многие процессы в живых телах являются стохастическими. Даже генетически идентичные клетки в одной ткани имеют разные уровни белковой экспрессии, разные размеры и структуру в силу стохастической природы энергетического взаимодействия отдельных молекул в клетках. Стохастическая природа наследования признаков в «малом» кардинально отличается от детерминированного наследования признаков в «большом» (тема гештальт-биологии). Например, отпечатки кончиков пальцев у всех людей различны притом, что пальцы в «целом» детерминированы по форме и строению (3 фаланги и пр.). Тем самым, биологические феномены связаны с дуализмом «стохастика-детерминизм».
Согласно закону Менделя независимого наследования признаков, информация с уровня молекул ДНК диктует макроструктуры живых тел по многим независимым каналам несмотря на сильные шумы. Так, цвета волос, глаз и кожи наследуются независимо друг от друга. Соответственно, каждый организм является машиной многоканального помехоустойчивого кодирования. Автор полагает, что будущее биологии связано с изучением глубинной и закономерной системы вероятностей в мире стохастических энергий взаимодействия в материальных средах.
Выявление универсальных стохастических дихотомий в геномах позволяет по-новому осмысливать явления дихотомий в наследуемых конструкциях биологических тел. Например, почему на протяжении миллиардов лет жизни на Земли для бактерий и вообще прокариот типичным является размножение путем дихотомического деления тела именно на две половины? На какие структурно-энергетические основы опирается этот «вечный» дихотомический феномен размножения бактерий, который сопровождается сложнейшим процессом дихотомического разделения всей дихотомически организованной генетической информации вместе с сопровождающими ее многовидовыми белковыми и нуклеиновыми ансамблями бактериальной клетки?
Автор предлагает следующий возможный ответ на подобные вопросы: существует скрытый от непосредственного восприятия мир семейств вероятностей, структурированных на основе бинарных оппозиций (типа Инь-Ян), напоминающих, в частности, бинарные оппозиции в физике:
положительный и отрицательный электрический заряды, северный и южный полюса магнитов, силы притяжения и отталкивания и пр.
Именно по образу и подобию бинарно организованных семейств вероятностей этого многослойного мира строятся генетически наследуемые биологические тела. Образно говоря, наши тела являются как бы одеждой, надетой на эти бинарно структурированные семейства вероятностей, выступающие прототипами биологических структур и наделенные своими формами энергии. В определенной мере это аналогично ситуации с человеком-невидимкой из знаменитого романа Г. Уэльса, невидимая фигура которого проявлялась только при ношении им одежды. Это также напоминает представления о проявленном и непроявленном мирах и знаменитую аллегорию Платона о мире идей и тенях на стене пещеры, по которым люди, живущие в пещере, могут судить об истинном скрытом мире идей. Изучая с помощью математики алгебраические закономерности геномных ДНК, мы опосредованно исследуем закономерности этого скрытого мира бинарных семейств вероятностей, являющегося прародителем биологических структур с их удивительными свойствами.

Рис. 4. Иллюстрация к теме скрытого мира структурированных стохастик (изображение взято из сайта https://wink.ru/movies/chelovek-nevidimka-gerbert-uells-year-2020).
Fig. 4. Illustration to the theme of the hidden world of structured stochastics (image taken from https://wink.ru/movies/chelovek-nevidimka-gerbert-uells-year-2020).
Автор полагает, что - помимо алгебры – важным инструментом для исследования этого скрытого базового мира бинарно-структурированных семейств вероятностей является музыка с ее способностью эмоционального воздействия, вызывающего слезы, ощущения мурашек по телу и пр. Возникающие волнение и физиологические эффекты, видимо, связаны с тем, что, наслаждаясь хорошей музыкой, мы соприкасаемся с пленительной гармонией этого скрытого мира, отраженной, в том числе, в структурном устроении генетической системы с ее вечными и универсальными для всех организмов правилами бинарно-стохастической организации. Это же может объяснять феномены музыкальной терапии, влияния музыки на рост растений и протекание биотехнологических процессов (например, изготовления вина), а также издревле известную врожденную склонность людей к музыке (так, во Франции найдена флейта, которой, по меньшей мере, 32 тысячи лет).
Представление о закономерном мире бинарно-структурированных семейств стохастических процессов как основе наследуемых биологических структур важно, в том числе, для осмысления генетического интеллекта. Под генетическим интеллектом мы понимаем ту часть интеллектуальных потенций живых организмов, которая позволяет на основе генетической информации в молекулах ДНК и РНК выстроить, например, из одной оплодотворенной клетки организм с триллионами клеток так, что в нем многоканальным помехоустойчивым образом воспроизводятся родительские признаки, несмотря на сильные шумы и постоянно меняющиеся по ходу жизни условия питания и внешних воздействий. Речь при этом идет о систематическом росте по ходу онтогенеза количества параметров тела и соответствующем увеличении размерности его конфигурационного пространства состояний [6]. Данный подход перекликается со следующим мнением о деятельности мозга известного специалиста по искусственному интеллекту R. Kurzweil: мозг представляет собой вероятностный рекурсивный фрактал, который кажется чрезвычайно сложным, но фактически может оказаться, что он сконструирован намного проще, чем кажется [7, c. 50].
С развитием физики и возникновением квантовой механики люди обратили внимание на принципиальную важность мира вероятностей для понимания и моделирования видимых ими объектов и процессов окружающей среды. Создатели квантовой механики П.Йордан и (позже) Э.Шредингер указывали на ключевое отличие живых тел от неодушевленных: неодушевленные объекты управляются средним случайным движением их миллионов частиц и движение отдельных частиц не существенно для целого; напротив, в живом организме избранные – генетические - молекулы обладают диктаторским влиянием на весь организм за счет квантового усиления [8]. Йордан утверждал, что упущенные наукой законы жизни являются законами вероятности квантового мира. Выявление описанных в данной статье и других публикациях автора универсальных правил стохастической организации геномных ДНК можно рассматривать, как пример тех правил, существование которых прогнозировал Йордан.
Описываемые алгебро-генетические исследования дополняют тему важности мира вероятностей. Представленные исследования созвучны работам В.В. Налимова [9], который считал своей целью построение вероятностной модели языка, а затем и сознания в целом.
Изложенный выше результативный метод иерархии бинарных стохастик представляется важным для многообразных применений в генетике и биологии. Его особенностью является то, что он представляет информационную последовательность (генетическую или иную) не как однострочный текст, а как многослойный набор множества текстов, каждый из которых написан на своем n-плетном алфавите. Соответственно, в описанном случае геномная ДНК выступает как полиглот, несущий послания одновременно на множестве разных алфавитов.
Такое представление геномных ДНК для изучения их стохастических закономерностей напоминает традиционную русскую матрешку, в которой фигуры разных размеров вложены друг в друга, образуя единое целое (Рис. 5). В свете этой аналогии описанный авторский метод геномного анализа может упрощенно называться «методом стохастической матрешки» (отчасти данный метод ассоциируется также с ярусным устройством традиционных индийских музыкальных инструментов – ситаром, сародом и сантуром -, которые наряду с основными струнами имеют лежащие под ними дополнительные наборы резонирующих струн, что придает индийской музыке особое звучание).

Рис. 5. Русские матрешки как иллюстрация авторского метода иерархий бинарных стохастик для исследования геномных ДНК.
Fig. 5. Russian nesting dolls as an illustration of the author's method of binary stochastic hierarchies for the study of genomic DNA.
По имеющимся у автора результатам этот метод полезен для познания и сравнительного анализа не только длинных геномных ДНК, но также относительно коротких ДНК генов, в которых дихотомии процентов n-плетов водородных связей нарушаются. Он позволяет сопоставить ДНК каждого генома и каждого гена, образно говоря, «отпечаток пальца» стохастической организации ее бинарных представлений и в этой связи приписывать ДНК и РНК каждого генома и каждого гена индивидуальный «полиплетный стохастический паспорт». Такая полиплетная паспортизация квази-стохастических генетических последовательностей представляется полезной для выявления отношений структурного родства генетических объектов. Желательна организация международного проекта по ней.
Данный метод представляется полезным также для развития «бинарно-стохастической ритмологии» (или «ритмологии стохастических матрешек») в связи с тем, что многие физиологические ритмы при ближайшем рассмотрении связаны с бинарными последовательностями и стохастическими флуктуациями в них в силу стохастики энергетических взаимодействий в молекулярных средах. Например, последовательности сердечных пульсаций характеризуются стохастическими флуктуациями кардиоинтервалов в них. Эти флуктуации кардиоинтервалов, имеющие диагностическое значение, можно исследовать названным методом с целью выявления стохастических закономерностей типа дихотомий вероятностей соответствующих n-плетов в их бинарных представлениях. В целом, названный авторский метод анализа последовательностей ДНК ведет к новым полезным подходам для развития эволюционной биологии и персональной генетики, а также разных ветвей физиотерапии, фармакологии, арт-терапии и медицинской инженерии. В частности, он успешно применен автором в анализе стохастической организации длинных фонетических последовательностей русского языка (то есть последовательностей звуков четырех видов - кратких и долгих гласных, глухих и звонких согласных) на материале объемных текстов романов А.Н.Толстого, Ф.М.Достоевского, А.С.Пушкина, русского текста Библии и пр. [10]. В таких фонетических последовательностях звуков четырех видов также по методу стохастических матрешек обнаружены дихотомические деревья вероятностей (по аналогии с описанными стохастическими закономерностями геномных ДНК). На этом пути познания биологического значения полиплетных стохастических закономерностей в генетический и физиологический анализ вводятся алгебраические формализмы и модели матричной генетики, метрического анализа, квантовой информатики, алгебраической геометрии, теории резонансов и теории антенных решеток [1-4, 6, 10].
Знаменитая книга «Игра в бисер» 1942 года Нобелевского лауреата по литературе Г. Гессе посвящена игре, цель которой найти глубинную структурно-математическую связь между предметами из разных областей науки и искусства [11]. По сути своей, «игра в бисер» представляет собой искусство сочинения метатекста, синтез всех отраслей искусства в одно, универсальное искусство (https://ru.wikipedia.org/wiki/Игра_в_бисер). Речь идет, прежде всего, о связи музыки и математики и о времени, когда музыкальные процессы стали выражать физико-математическими формулами. По нашему мнению, генетические тексты ДНК с их скрытыми закономерностями являются теми метатекстами, на которых строятся биологические тексты различной природы. Наши поиски адекватного алгебро-числового подхода для анализа и синтеза музыкальных и других произведений можно рассматривать как продолжение мыслей и убеждения множества музыкантов и мыслителей о связи музыки и математики.
В данной статье внимание акцентируется на водородных связях также потому, что они являются одним из важнейших компонентом живого и представлены во многих биологических структурах. В частности, как известно, они во многом определяют пространственную конфигурацию белков и являются важным фактором в функционировании ферментов, которые управляют молекулярными процессами в биологических телах. Нобелевский лауреат Л. Полинг полагал, что по мере дальнейшего применения методов структурной химии к физиологическим проблемам будет обнаружено, что значение водородной связи для физиологии больше, чем значение любой другой отдельной структурной особенности [12]. Мы полагаем, что на системах водородных связей и их объединений в солитоно-подобные структуры строится стохастическая протосистема биологической регуляции [13, 14]. Водородные связи определяют многие свойства воды и льда. Богатство эмерджентных свойств систем водородных связей можно иллюстрировать примером медуз, которые на 98% состоят из воды, представляя собой, образно говоря, сложно форменный мешок с водяным субстратом водородных связей. При этом медузы являются самыми древними многоклеточными животными Земли с огромным эволюционным разнообразием видов и функциональных возможностей, включая возможности полового и бесполого размножения. Добавим, что водород – самый распространенный элемент во Вселенной: на его долю приходится около 88,6 % всех атомов.
Выявление универсальных правил квази-стохастической организации последовательностей водородных связей 2 и 3 в геномных ДНК дает дополнительное основание для усиленного интереса к водородной медицине, интенсивно развиваемой во многих странах, начиная с 2007 года. В том числе работы по водородной медицине ведутся в лаборатории автора с использованием активирующих акустических и вибрационных воздействий в интересах медицины, растениеводства и ветеринарии. К настоящему времени среди более 1000 публикаций в мире по воздействию водорода на организм человека нет ни одной о его вредном или побочном воздействии. Здесь можно напомнить, что в кишечнике человека ежедневно производится до 12 литров газообразного водорода.
В целом статья показывает, что, стартуя от проблем музыкальной гармонии, можно прийти к глубочайшим универсальным секретам живой материи с целью развития эволюционной биологии, персональной генетики, инженерной медицины и синтеза разных видов искусств. Рис. 6 иллюстрирует идею музыкальной гармонии в организации живого, условно представляя тело человека в разных возрастах как музыкальный синтезатор.
Рис. 6. К теме биологического значения музыкальной гармонии
Fig. 6. On the theme of the biological significance of musical harmony
ЗАКЛЮЧЕНИЕ
- Параметрическое строение системы водородных связей геномных ДНК структурно сопряжено с отношениями музыкальной гармонии пифагорейских квинтовых строев;
- В стохастической организации последовательностей водородных связей геномных ДНК высших и низших организмов реализуются описанные универсальные правила процентных дихотомий;
- Стохастическая организация геномных ДНК опирается на сети фрактальных деревьев, основанных на дихотомиях процентного состава n-плетных представлений этих ДНК;
- Авторский метод иерархий бинарных стохастик является результативным и перспективным для дальнейших применений в генетике и эволюционной биологии;
Результаты исследований универсальных закономерностей стохастической организации геномных ДНК позволили выдвинуть авторскую концепцию скрытого мира закономерных стохастических структур как прототипов и основ биологических организмов.
1. Petoukhov S.V. Hyperbolic Numbers in Modeling Genetic Phenomena. Preprints 2019, 2019080284 (doi:https://doi.org/10.20944/preprints201908.0284.v4). (2020). https://www.preprints.org/manuscript/201908.0284/v4
2. Петухов С.В. (2008). Матричная генетика, алгебры генетического кода, помехоустойчивость. - Москва, РХД, 316 с. http://petoukhov.com/ matrix-genetics-petoukhov-2008.pdf. [Petoukhov S.V. Matrix genetics, algebras of the genetic code, noise immunity. Moscow, RHD, 2008, 316 p. (In Russ.)]
3. Petoukhov S.V. The Genetic Coding System and Unitary Matrices. Preprints.org 2018, 2018040131. https://doi.org/10.20944/preprints 201804.0131.v2.
4. Petoukhov S.V., He M. (2023). Algebraic biology, matrix genetics, and genetic intelligence. Singapore, World Scientific (in print).
5. Иванов Вяч. Вс. (1978). Чет и нечет. Асимметрия мозга и знаковых систем. Москва, Советское радио, 184 с. [Ivanov Vyach. Vs. (1978). Even and odd. Asymmetry of the brain and sign systems. Moscow, Soviet radio, 1978, 184 p. (In Russ.)].
6. Петухов С.В. (2022). Генетический интеллект, доктрина энергоинформационной эволюции на основе био-антенных решеток и квантовая информатика. Биомашсистемы, т. 6, №4, c. 45-64. [Petoukhov S.V. Genetic intelligence, the doctrine of energy-informational evolution based on bio-antenna arrays and quantum informatics. Biomachsystems, 2022, vol. 6, no. 4, p. 45-64 (In Russ.)].
7. Tsang W.H. Fractal brain theory. Lulu.com, 2016, 530 p. ISBN 978-1-326-75322-1.
8. McFadden, J. and Al-Khalili, J. (2018). The origins of quantum biology. Proceedings of the Royal Society A, Vol. 474, Issue 2220, pp. 1-13. (https://doi.org/10.1098/rspa.2018.0674).
9. Налимов В.В. (2015). Разбрасываю мысли. В пути и на перепутье. Москва, Центр гуманитарных инициатив. [Nalimov V.V. I scatter my thoughts. On the road and at the crossroads. Moscow, Center for Humanitarian Initiatives, 2015 (In Russ.)], ISBN 978-5-98712-521-2.
10. Petoukhov S.V. (2018). Structural Connections between Long Genetic and Literary Texts. Preprints 2018, 2018120142, DOI:https://doi.org/10.20944/preprints 201812.0142.v2
11. Гессе Г. (2022). Игра в бисер. Москва, АСТ (Hesse H. The Glass Bead Game, Moscow, 2022, AST), 978-5-17-075534-9.
12. Pauling, L. (1940). The Nature of the Chemical Bond and the Structure of Molecules and Crystals: An Introduction to Modern Structural Chemistry, 2nd ed. (Oxford University Press).
13. Петухов С.В. (1999). Биосолитоны. Основы солитонной биологии. -Москва, ГП Кимрская типография. 288 с. [Petoukhov S.V. Biosolitons. Fundamentals of soliton biology. - Moscow, Kimry Printing House, 1999, 288 p. (In Russ.)] http://petoukhov.com/?page_id=278
14. Petoukhov S.V. (2022). The Principle "Like Begets Like" in Molecular and Algebraic-Matrix Genetics. Preprints 2022, (https://www.preprints.org /manuscript/202211.0528/v3), from 23 May 2023.








